Imaging a supermassive black hole and extracting physical information requires good knowledge of both the gravitational and the astrophysical conditions near the black hole. When the geometrical properties of the black hole are well understood, extracting information on the emission properties is possible. Similarly, when the emission properties are well understood, extracting information on the black-hole geometry is possible. At present however, uncertainties are present both in the geometry and in the emission, and this inevitably leads to degeneracy in the interpretation of the observations. In this work, we explore here the impact of varying geometry and emission coefficient when modelling the imaging of a spherically-accreting black hole.
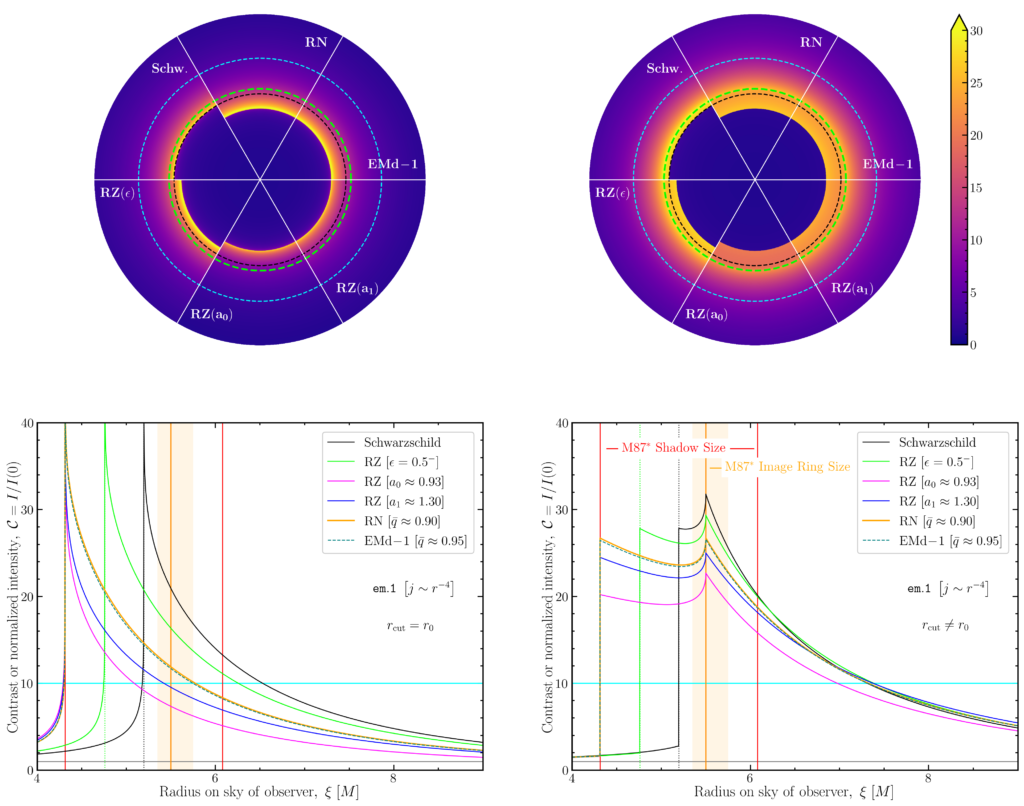
In the figure, we show the variation of the normalized intensity, or (intensity) contrast, when the black hole is undergoing cold spherical accretion (Bondi-Michel). This cold (free-fall) accretion model can be described analytically, allowing us to vary only the emission coefficient of the accreting material. In the left columns, we assume that the emission zone extends all the way down to the event horizons whereas in the right columns the emission is suppressed close to the photon sphere. The sharp drop in contrast invariably marks the shadow boundary with the peak in the contrast indicating the size of the ring-like feature observed by the EHT in the 2017 image of M87*. The figure shows black holes with the same shadow size but differing spacetime geometries can be distinguished in principle. While we show the scenario for a particular emission model here, the paper considers various other simple power-law emission models.
Adopting the Rezzolla-Zhidenko parametric metric to model arbitrary static black-holes, we first demonstrate how shadow-size measurements leave degeneracy in the multidimensional space of metric-deviation parameters, even in the limit of infinite-precision measurements. Then, at finite precision, we show that these degenerate regions can be constrained when multiple pieces of information, such as the shadow-size and the peak image intensity contrast, are combined. Such degeneracy can potentially be eliminated with measurements at increased angular-resolution and flux-sensitivity. While our approach is restricted to spherical symmetry and hence idealized, we expect our results to hold also when more complex geometries and emission processes are considered.